Example
:- What power supply would be suitable to run a 50W
transceiver from a 12V power supply?
from P = V x I
we
get 50 = 12 x I
then I = 50 / 12
result 4.166
Amps
The answers
given in the exam might be :-
A 12V at 500mA
B 12V at 1A
C 12V at 6A
D 24V at 4A
D is wrong as it
is at the wrong voltage, A & B are two low so
the answer is C
However be aware
that the output power actually bares no direct
relationship to the input power as sometimes to
have an output of 50W RF you need 100W of DC input
!!!
Recall that a current through
a resistor results in a transfer of electrical
energy to heat energy in the resistor.
Because resistance is
the opposition to the flow of electrons the energy of
the electrons being slowed down results in the
generation of heat in the resistor. This is why
resistors have a resistance value and a power wattage
to indicate how much power they can dissipate.
Understand
the relationship between potential difference,
current and resistance. Manipulate the equation V =
I x R to find the unknown quantity given the other
two. The prefixes milli and kilo may be used.
In
the FLC you were introduced to a magic triangle this is
also needed in the ILC so that you can manipulate the
equation V = I x R to find the unknown item given the
other two items.

Practice with this until you are certain that you fully
understand how to find the one unknown from two know
items.
NOTE: calculations in the exam may use the prefixes
milli and kilo.
Again student from an early course suggested the
following to help you remember the order of the letters
:-
V =
Vanilla I = Ice-cream R = Ready
hence
Vanilla Ice-cream Ready
Understand
circuits comprising series and parallel connections of
resistor and cells.
Calculate
currents and potential differences in such circuits.
The
circuit below Fig1 the Resistors R1, R2 and R3 are the
opposition to current flow around the circuit to find
the current flowing in the circuit one must first work
out the total resistance value.
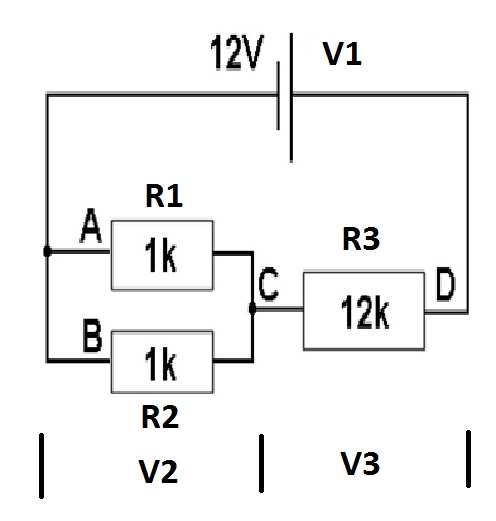
Fig1