Bredhurst Receiving and Transmitting Society

3. Technical Basics

Alternating currents and voltages

3f.1 Understand the sine wave curve as a graphical representation of the rise and fall of an alternating current or voltage over time and that both the frequency and the amplitude must be specified.

Recall that the time in seconds for one cycle is the Periodic Time (T) and the formula T=1/f and f=1/T where f is the frequency in Hz.

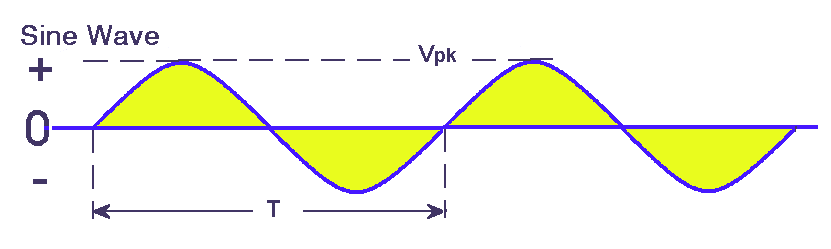
A sine wave is a pure wave and contains no harmonics. Any deviation from the pure sine wave curve is indicative of other products mixed in with the signal e.g. harmonics.

To fully describe a sine wave both the amplitude and the time for 1 cycle ( also called the periodic time ) or the number of cycles per second, the frequency in Hertz Hz must be specified.

However voltage quoted could be a peak to peak value or might be the RMS value.

The time taken for one complete cycle is known as the Periodic Time (T)...however frequency is the more commonly used term.

The relationship between Periodic Time (T) and Frequency ( f in Hz) can be expressed like so:

T = 1/f or transposing it to give f = 1/T where f is in Hertz.

It is worth pointing out that in earlier times the frequency was measured in Cycles per Second ...these days Hertz, abbreviated to Hz is now used.....in honour of an early experimenter in the electrical field.

Recall that the power dissipated (in a resistive circuit) varies over the cycle and that the RMS current or voltage is equal to the current or voltage of a DC supply that would result in the same power dissipation as that of the AC sine wave current or voltage.

Recall that the RMS value of a sinusoidal voltage is given by Vpk/√2 (Vpk x 0.707).

When dealing with D.C the power dissipated in a resistive circuit is constant and one way it can be calculated is to multiply the applied voltage by the current flowing in the circuit. However when using an AC waveform the voltage is not constant but varies with the frequency. It follows that the current must also vary with the frequency of the applied voltage. Therefore the calculation of power dissipated in an AC circuit is not straight forward. To calculate the power dissipated in an AC circuit the RMS (Root Mean Square) voltage must be used.

The RMS voltage is one that will the produce the same equivalent heating in the circuit as would an equivalent DC voltage. RMS voltage measurements can be assumed unless otherwise stated.

How do we calculate the RMS value of a waveform if we only know the Peak value (Vpk)

You need to be able to recall that RMS value of a sinusoidal voltage is given by Vpk/√2

then √2 = 1.414

and 1 / 1.414 = 0.707 So RMS (Vpk x 0.707).......

Simple just multiply the peak value by 0.707

3f.2 Recall that by repeatedly charging and discharging in alternate directions, a capacitor can pass alternating currents, but cannot pass a direct current.

Recall that the ratio of the RMS potential difference to the RMS current as the capacitor stores energy in its electric field is called the reactance of the capacitor and is measured in ohms.

Applying a DC voltage across the plates of a capacitor will charge the capacitor with electricity. The capacitor can hold a charge for a long time...indefinitely in the case of a perfect capacitor with no losses.

When the DC voltage is applied there is an in rush current that charges the capacitor. Once the capacitor is charged no further current will flow....in fact all current flow stops. A capacitor cannot pass DC once it is charged.

When an AC supply is applied to the plates of a capacitor there will be an in rush of current just as on DC, however once the supply changes polarity as the waveform reverses then the capacitor must discharge and then recharge in the opposite polarity. When the supply again changes polarity as the waveform reverts back the capacitor must again discharge and re-charge again in the opposite sense. So when you apply an AC waveform to a capacitor current is constantly charging and discharging the capacitor and flowing around the circuit.

The ratio of the AC voltage to the current flowing in the circuit as the capacitor stores energy in its electric field is called the reactance of the capacitor and is measured in ohms.

3f.3 Recall that an inductor will take time to store or release energy in its magnetic field.

Recall that the ratio of the RMS potential difference to the RMS current as the inductor stores energy in its magnetic field is called the reactance of the inductor and is measured in ohms.

Just like a capacitor can store energy in its electric field (between the plates of the capacitor) an inductor (a coil of wire) stores energy in its magnetic field. An inductor has a strange quality (inductance) which makes it oppose any change in the current flowing through the inductor. So when you apply a voltage (AC or DC) to an inductor the current can only build up slowly as the inductor fights the change in the "status quo".

Just as in a capacitor, the ratio of the AC voltage to the current flowing in the inductor circuit as the magnetic field builds up and collapses in time with the frequency is called the reactance of the inductor... and is also measured in ohms.

3f.4 Recall that in a circuit comprising capacitors and resistors, or inductors and resistors, a current will result in energy transfer (into heat) in the resistors and energy storage and release in the capacitors or inductors.

Recall that in such a circuit the ratio of the overall potential difference to current is termed ‘impedance’ and that this name denotes an opposition to both energy transfer and energy storage in the circuit. Recall impedance is measured in ohms.

In a circuit comprising capacitors and resistors, or inductors and resistors, the current that flows on account of the AC voltage applied will result in energy transfer in the resistors (they will get hot!) and energy storage and release in the capacitors, as an electric field, or in the inductors as a magnetic field. Storing energy of course does not consume any power...but forcing current to flow through a resistance (as the name implies) does consume power!

In such circuits containing resistance and or capacitance and or inductance the ratio of the overall potential difference to current flowing is termed 'impedance'. This name denotes an opposition to both energy transfer and energy storage in the circuit. Note this impedance to the flow of AC is measured in ohms.