|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
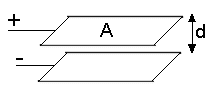
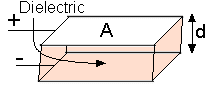
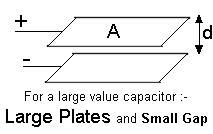
Syllabus Sections:- Capacitance 2D1 9 Understand the factors influencing the capacitance of a capacitor; area and separation of the plates, permittivity of dielectrics and formula C = K A /d. Note the wording of the syllabus:- Understand the factors influencing the capacitance... By saying Understand ...... the formula C = K A /d calculations using the formula can be required. In the Intermediate Licence course you learned that a capacitor consists of two metal plates separated by an insulating material. In its simplest form is two metal plates set parallel to each other with a separation gap of insulating material. This material is called a dielectric. The capacitance is the word used to describe the ability of the two plates to store an electrical charge. The capacitance is proportional to the area of the plates (marked A in the diagram) and inversely proportional to the distance between the plates (marked d in the diagram) and also on the properties of the dielectric between the plates. The dielectric can be as simple as air but other materials used are paper, rubber, polythene, mica and ceramics. Thus the bigger the area the bigger the charge the capacitor can hold but the bigger the gap the smaller the charge that can be held. So the ideal high value capacitor will have large plates and a very small gap between them.
|
||||||||||||||||||||||||||||||||||||||
|
Dielectric material |
Use |
Breakdown voltage |
Stability |
Frequency |
|
Air |
Mainly used for variable tuning capacitors capacitance values up to say 1000pf |
High |
Good |
up to say 300MHz |
|
Electrolytic semi liquid compound |
Used for very high value capacitors in Power supplies for smoothing |
High |
Good |
up to 1MHz |
|
Paper |
Used in high voltage capacitors |
High |
Good |
up to 20MHz |
| Mica | This is the best dielectric but is expensive |
Good |
Very Good |
up to and higher than 200MHz |
|
Polyester |
The usual type of capacitor when critical values are not required such as audio coupling and decoupling. Tolerance typically 20% |
Medium |
Fair |
up to about 100 kHz |
|
Ceramics |
High dielectric constant and has good temperature stability |
Medium |
Good |
up to 150 - 200MHz |
2D7 11 Understand the charging and discharging of a capacitor in a CR circuit and the meaning of the time constant T=CR.
Questions heavy on
maths are very likely in this section of the syllabus
Capacitance
Charge and discharge of Capacitors in CR circuits
In this section we are going to use the maths notation that if two items need to be multiplied together then they are written together without the times (X) symbol. Thus V = I x R would be written as V = IR
Charge Q (measured in Coulombs) on a capacitor
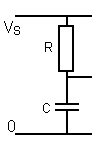
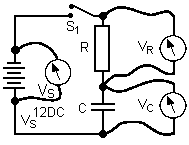
Consider the circuit arrangement shown below
and the following equations:-
Equation A
The charge Q on a capacitor is equal to the Potential Difference (V) in VOLTS across the capacitor TIMES its capacitance (C) in FARADS
Q
= CV
To put some figure on this a capacitor of 1F will store 1C of charge for an applied p.d. of 1V
thus
1C = 1F x 1V
Equation B
The charge in Coulombs, is equal to the current in amps X the time that the current has flowed in SECONDS
Q = Amps x Seconds
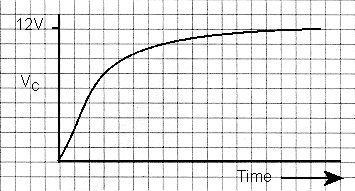
Now looking at the diagram above before S1 is closed, VR = zero, VC = zero
Then at the instant S1 is closed, no current has flowed into the capacitor, therefore there is no charge Q and VC = zero.
VR = 12V and by Ohm's law current (I) starts to flow and I = VS / R Amps at that instant.
A short time after S1 is closed a current is flowing, therefore C is charging, VR must be falling because VC + VR = 12V
VR is now VS - VC.
If VR is less then IR is less and the rate of charge of the capacitor falls, until eventually the capacitor is charged to 12V and no current flows then VR = zero.
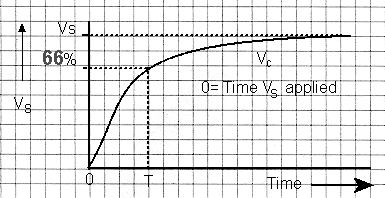
The graph of VC with respect to time is shown and is known as an EXPONENTIAL CURVE
Time Constant
You will need to have a basic mathematical appreciation of the foregoing paragraphs in order to be able to understand existing circuits involving C and R, and to be able to select values to give correct function in your own circuits.
With Q = Amps x Seconds and Q = CV then
IT = CV thus T = CV/I, from ohm's law R = V/I so T = CR
So the equation is simply :-
T (in seconds) = C (in farads) x R ( in ohms)
where T is the time taken for a capacitor to charge to 66% of the applied voltage VS
|
|
|
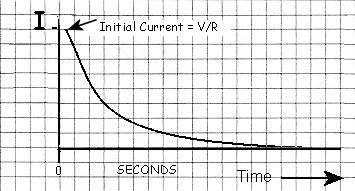
T is called the Time Constant, and equally applies to the charge of a capacitor and the discharge of a charged capacitor via a resistor where similarly discharge by 66% of VS occurs in Time T = CR
Example:
How long will it take to charge a capacitor of one microfarad to 66% of the applied voltage, via a resistor of 2 megohms ?
T
= CR 
Using the exponential notation
T = 1 x 10-6 x 2 x 106
the 10-6 and 106 cancel each other out and the answer is
1 x 2 = 2 Seconds
T = CR applies to timer circuits like the well known NE555 timer, PSU smoothing circuits, decoupling circuits, delay and de-bounce circuits.
Let's work through another example as it may help you to understand it better.
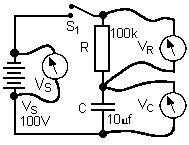
Whilst under steady state conditions the perfect capacitor presents an infinite resistance to DC voltages however when the capacitor is in a timing circuit the capacitor offers no resistance, it allows current to flow as follows:-
At the instant S1 is closed the current will be 1milliamp (by Ohm's Law I= V/R = 100 /100,000 = 1/1000 - 1 mA
C starts to charge and builds up a voltage.
When the charge on C reaches 50VC, there is 50V left across R and thus the current I is now 50/100,000 = 1/2000 = 0.5mA and thus C is charging slower.
The slow changing voltage curve is called an EXPONENTIAL curve.
At a time T = C (in FARADS ) X R (in OHMS) C = 10 micro F R = 100k
so
T = 10 X 10-6 X 100 X 103
T = 101 x 10-6 X 102 X 103
T = 106 X 10-6
T = 1 SECOND, the voltage on C will be ABOUT 2/3 of the initial voltage of 100 V = 66 Volts.
Not in the 2021 Full Syllabus Recall and apply the formulae for calculating the combined values of capacitors in series and in parallel
![]()
![]()
![]()
When
capacitors are linked in series the total value can be
calculated from the formula:- 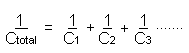

The
special case is when there are two capacitors linked in
series then the simplified formula can be used :- ![]()
When
capacitors are linked in parallel the total value can be
calculated from the formula:- ![]()

![]()