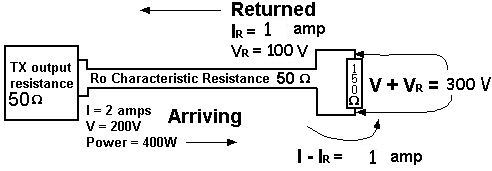
Before we go into the syllabus here is anexplanation of Standing Wave .

We have added this section so that you can have a grasp of what STANDING WAVES are.

must be obeyed even though we are dealing with aerial feeders.

Let's look at this from the point of view of the Transmitter (Tx). The Tx does not know what exists at the far end of the transmission line, so 200V/2A signal travels down the transmission line, building up an electromagnetic field, at a velocity close to that of light (for a good transmission line).

The signal then has an awkward situation to overcome when its wave front arrives at the 150 load, as there is a gross breach of . 150 cannot accept 2A under a pressure of a mere 200V. From we would need V = 150 x 2 = 300 V to satisfy the situation.

The back pressure across the load rises above 200V and starts sending current back into the line, in opposition.

The return current reduces the current flowing into the load, easing the situation.

Looking at the situation from the resistor load towards the Tx - there is the same cable with R_o = 50 so the ratio of the surplus voltage at the load and the return current must still be equal to Ro!

BUT how much current is going back ?

Now for the maths - for those who only want the final resultant equations skip down to after ( Equation 3 ).

So for those of you who are still with us here goes................

Let I_R = Return current, and V_R = Voltage needed to return that current.

So from again V_R / I_R = R_o (R_o in case you had forgotten is the Characteristic Resistance of the feeder cable)

We have the initial Voltage V = 200 and initial Current I = 2 but as R_o is common to the initial V and I and V_R and I_R then stating it mathematically

( Equation 1 )

V + V_R MUST fulfill

so ( R = the load resistance) ( Equation 2 )

The equations 1 and 2 are simultaneous and solving them gives us :-

( Equation 3 )

We should all be back together now !!!

So back to our example

From ( equation 3 )

( Equation 4 )

again thus

( Equation 5 )

So the voltage across the load is V + V_R = 300V

And the current into the load is I - I_R = 1 amp so

power into load is 300 watts

AND

Power arriving is 2 amps with pressure of 200 volts thus 2 x 200 = 400 watts

Power returning (which we have just found out is 1 amp with pressure of 100 Volts) 1 x 100 = 100 watts

400 - 100 = 300 watts is satisfied !!

a purely resistive load

For a line with a purely resistive load (i.e. load containing only resistance), SWR = R / Ro or Ro / R (whichever gives a value of 1 or greater).

The SWR is directly related to the amount of mis-match between the characteristic resistance and the load. The higher the mis-match, the higher the SWR.

For this example SWR = R / Ro = 250 / 50 = 5

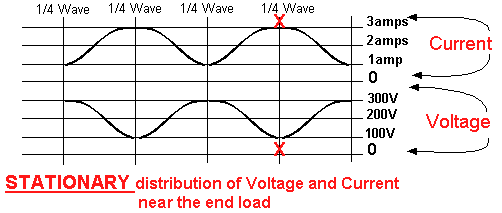
Re-drawing the original diagram, with the new information added we have :-

The reflected wave, current and voltage, alternately adds to and subtracts from the 2A/200V travelling from the Tx to the load.

Starting with 1 amp / 300 volts at the load now move back a 1/4 wave towards the Tx, the original and reflected wave are a half wave apart (total journey to and from the load) and 180⁰ in phase - the two current are in phase, giving 3 amps and the voltages subtract giving 200V - 100V = 100V at a distance of 1/2 wavelength, phase difference is 360⁰ and we are back to the conditions at the load 1 amp /300V.

At intermediate points there are different phases so the net current and voltages vary in a wave like manner (not a pure travelling sine wave) see the diagram below.

The net current and voltage varies along the length of the transmission line. The high and low voltage points are in fixed positions. If the transmitter output is a pure sine wave, the forward and reflected waves are pure travelling sine waves. The forward and the reflected waves interact causing a resultant waveform which is a stationary wave called "STANDING WAVE". As mentioned above this standing wave is not a pure sine wave.

So this static wave are not travelling waves like those causing them and can be measured by running a voltmeter along the transmission line. The standing wave ratio is 300:100 = 3:1 (max volts / min volts).

NOTE:- At point X X a 1/4 wavelength back from the load, the resistance R = V / I = 100 / 3 = 33.3.

If we cut off the load resistance and 1/4 wave length of feeder line, we could fit a 33.3 resistor at that new point and the Tx would not know that a change had taken place. The load still looks like 300.

The cable is now acting as a 3:1 transformer as well as a transmission line !!

To complete this section we will deal here with :-

Quarter Wave Transformer

In our example a load resistor of 3 x the characteristic resistance of the transmission lines 3 R_o at one end is transformed to R_o / 3 at the other.

In case you had forgotten the Tx in our case was 100 and load resistance of 300 and characteristic resistance of the line 100

Multiply the end values together 3 R_o x R_o/3 = R_o²

THE SAME RESULT IS OBTAINED FOR ANY LOAD RESISTANCE.

Let the resistance at one end = R to be transformed to R₁ at the other end

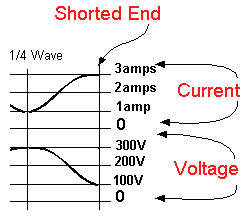
R₁ x R = R_o² so required R_o =

We use a quarter wavelength of line having a characteristic resistance

equal to

Example. to make a 2000 load look like an 80 we use a quarter wavelength of line with characteristic resistance

A quarter wave transformer always has a standing wave along it.

To be correct we should be dealing in impedances as we cannot avoid reactances so the equation becomes :-

Z_o² = Z_IN X Z_OUT and we will have more on this on another page 

Quarter Wave Stubs

If we put what would be a DC short at the end of a Quarter Wavelength of transmission line, and apply the correct frequency to the OPEN end, there will be maximum current and zero volts at the shorted end.

Moving back from the shorted end to the open end when we get to a 1/4 wave length back , there will be zero current and maximum volts, which indicates A VERY HIGH IMPEDANCE.

We can attach this stub anywhere along a working transmission line, it will have no effect despite the fact that at DC is looks like a short.

This stub is used to support transmission lines ( at one frequency only ). it can be shown that at lengths between 1/4 wave and the short the stub presents an inductive reactance, decreasing as we move towards the short.

Similarly, an open circuit stub presents a capacitive reactance which decreases as the open end is approached.

The two reactance stubs can be used to cancel out unwanted reactance in a system and are particularly applicable at microwave frequencies.

In the original example, the resistance a 1/4 wavelength back from the load is 33.3 ohms. The 1/4 wavelength transforms the impedance from 300 ohms to 33.3 ohms, but the SWR stays the same. SWR = Ro / R = 100 / 33.3 = 3.